Math Data Types

4.4. Math Data Types#

Vitis HLS supports most of the simple as well as composite C/C++ data types. Details of how different data types are synthesized are available in [AMD-Xilinx24c]. For DSP applications, we are most interested in arithmetic data types, such as the standard C/C++ integer and floating point data types as well as fixed-point data types supported by Vitis HLS. In this section, we focus our discussions on these math data types as well as the math operators and functions that operate on them.

4.4.1. Integer Types#

Vitis HLS supports synthesis of all standard C/C++ integer types. The bit-widths of these types are listed in the table below:

Table 4.2 Vitis HLS-supported standard C/C++ integer type bit-widths#
Integer type	bit-width
`(unsigned) char`, `(unsigned) int8_t`	8
`(unsigned) short`, `(unsigned) int16_t`	16
`(unsigned) int`, `(unsigned) int32_t`	32
`(unsigned) long`, `(unsigned) long long`, `(unsigned) int64_t`	64

Tip

The header file <stdint.h> must be included in order to use the exact bit-width integer types (unsigned) int*_t.

Arithmetic operations with the standard C/C++ integer types follow standard C/C++ conventions. Vitis HLS automatically selects the smallest bit-width operator needed for synthesis.
- Example 1:
```
short a;
char b;
int c = a*b;
```
  Vitis HLS selects to synthesize a 24-bit multiplier to perform the multiplication operation and then converts the 24-bit product to 32-bit int type result.
- Example 2:
```
int a; 
long b; 
short c = a+b; 
```
  Vitis HLS first truncates the 32-bit a and 64-bit b to corresponding 16-bit short versions, and then uses a 16-bit adder to perform the addition.
As shown in the examples above, Vitis HLS automatically selects the operators as well as the PL resources to implement the selected operators. However, the implementation choice made by Vitis HLS may be overridden using #pragma HLS bind_op.
Vitis HLS also supports arbitrary precision (AP) signed and unsigned integer types ap_int<W> and ap_uint<W> in C++, where W is the bit-width that can range from 1 to 1024. To use the AP integer types, the header file <ap_int.h> must be included. In addition, the maximum bit-width can also be extended to 4096 by defining the macro AP_INT_MAX_W before including the header file as below:
```
#define AP_INT_MAX_W 4096
#include <ap_int.h>
```
Again, Vitis HLS automatically synthesizes the smallest bit-width operator needed to implement a specific arithmetic operation. However, the operator does not need to conform to a bit-width that is an integer multiple of a byte (8 bits) for AP integers.
- Example 3:
```
ap_int<100> a;
ap_int<33> b;
ap_int<200> c = a-b;
```
  Vitis HLS first extends a and b to corresponding 101-bit AP integers, then uses a 101-bit subtractor to perform the subtraction, and finally extends the difference to a 200-bit AP integer.
- Example 4:
```
ap_int<100> a; 
long b; 
ap_int<100> c = a/b; 
```
  Vitis HLS selects to synthesize a 100-bit divider to perform the division operation. The long type variable b is first extended to a 100-bit AP integer and then the division is performed.
The ap_int<> and ap_uint<> classes support many standard binary, unary, logic, and bitwise operations. They also provide many helper methods for printing and conversion to standard C++ types. The details of all these can be found in [AMD-Xilinx24c] or from here.

4.4.2. Floating Point Types#

Vitis HLS supports the standard C/C++ float and double types as well as the half-precision type half for synthesis with IEEE-754 standard partial compliance [AMD-Xilinx20]:

Table 4.3 Vitis HLS-supported floating-point types#
Floating-point type	bit-width	mantissa bit-width	exponent bit-width	sign bit
`half`	16	10	5	1
`float`	32	23	8	1
`double`	64	52	11	1

Tip

The standard C++ type long double is also supported, but Vitis HLS gives the exact same implementation as double. Hence, there is no point to use long double.

The following unions defined in this example may be employed to access mantissa and exponent components of half, float, and double variables:

typedef union {
  half fp_num;
  uint16_t raw_bits;
  struct {
      uint16_t mant : 10;
      uint16_t bexp : 5;
      uint16_t sign : 1;
  };
} half_num_t;

typedef union {
  float fp_num;
  uint32_t raw_bits;
  struct {
      uint32_t mant : 23;
      uint32_t bexp : 8;
      uint32_t sign : 1;
  };
} float_num_t;

typedef union {
  double fp_num;
  uint64_t raw_bits;
  struct {
      uint64_t mant : 52;
      uint64_t bexp : 11;
      uint64_t sign : 1;
  };
} double_num_t;

Vitis HLS also supports complex-valued extension types of the three floating-point types:
- std::complex<half>
- std::complex<float>
- std::complex<double>
The header file <complex.h> should be included to use these complex-valued types.
Arithmetic operations with floating-point variables are synthesized using floating-point IP cores [AMD-Xilinx20]. Typically, floating-point operations require significantly more PL resources and endure longer latencies that their counterparts for standard integer types.

Caution

The Vitis code analyzer does not support anaylsis of code that uses the half type. It needs to be switched off during the C simulation step.
As in the case of integer types, Vitis HLS automatically selects the operators and the PL resources to implement the selected operators. However, the implementation choice of some floating-point operators made by Vitis HLS may be overridden using #pragma HLS bind_op. For example, the bind-op pragma in the following C++ function
```
void top(double x1, double x2, double &y) {
#pragma HLS bind_op variable=y op=dmul impl=fabric
  y = x1 * x2;
}
```
changes the default implementation of the double multiplier from maxdsp to fabric, i.e., to implement the multiplier without using any DSP resource in the PL. In this case, a lower latency can be achieved.
One may also use the latency= option to override the default latency Vitis HLS assumes for an operator. This may come handy to tell Vitis HLS to use a longer latency for the operator when the default RTL design provided by Vitis HLS produces negative slacks.
The Vitis HLS Math Library hls_math implements synthesizable bit-approximate versions of most math functions in the standard C++ cmath library. The list of functions supported can be found here.
- Three versions of each function, one each for half, float, and double, are provided in the library. All these versions can be used in synthesis as well as simulation. To use them, the header file <hls_math.h> should be included and the namespace hls should be used. For example, the half, float, and double versions of the standard cosine function are hls::half_cos, hls::cosf, and hls::cos, respectively.
- Using the version of a function corresponding to the argument type typically saves PL resources and reduces latency since not type conversion is needed, and the implementation is usually faster and smaller for the lower precision versions.
- Since the bit-approximate implementation of a function in the Vitis HLS Math Library may use a different underlying algorithm, it may not provide the same accuracy of the standard C++ math library counterpart. In order to match the RTL simulation and test bench golden results in the co-simulation step, we should always use functions in the Vitis HLS Math Library in both the DSP kernel code and the test bench code.
Start from v2024.2, Vitis HLS also support arbitrary precision float types using the template ap_float<W, E>, where W is the total bitwidth and E is the bitwidth of the exponent, leaving 1 bit for sign and the remaining W-E-1 bits for the mantissa. Standard arithmetic operators and a small subset of math functions are supported for the AP float types. The header file <ap_float.h> must be included to use the AP float types. More details of the AP float point types can be found here.

4.4.3. Arbitrary Precision Fixed Point Types#

Vitis HLS supports AP fixed-point types that are declared using the C++ class templates ap_fixed<W,I,[Q,O,N]> and ap_ufixed<W,I,[Q,O,N]>, where the arguments are specified in the table shown in the figure below: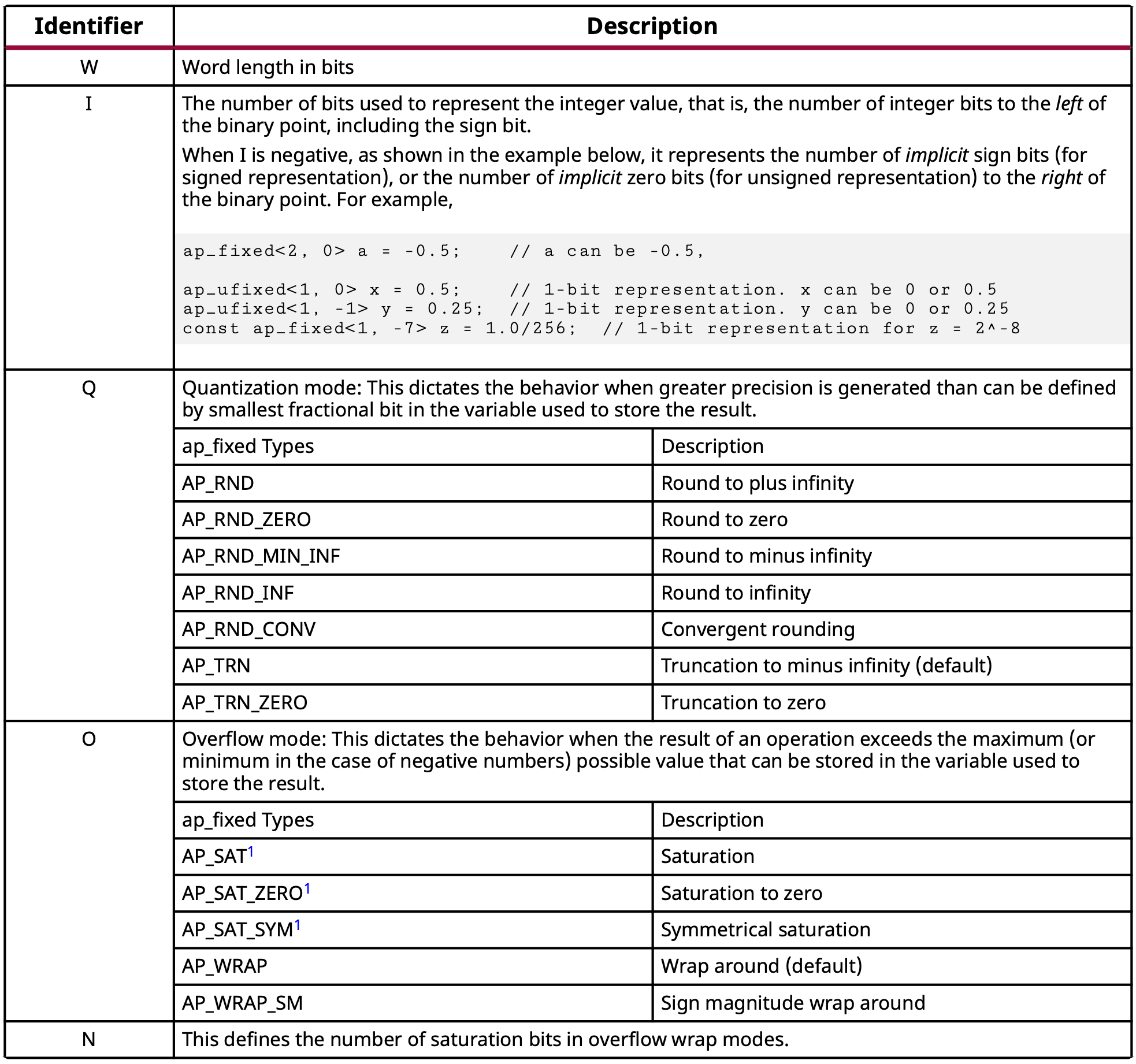

Fig. 4.3 Arbitary precision fixed-point type identifiers (table taken from [AMD-Xilinx24c])#
To use the AP fixed-point types, the header file <ap_fixed.h> should be included. Exactly the same as the AP integer types, the default maximum bit-width is 1024 and can be extended to 4096 by defining the macro AP_INT_MAX_W to that maximum value.
Again the same as for the AP integer types, Vitis HLS automatically synthesizes the smallest bit-width operator needed to implement a specific arithmetic operation involving the AP fixed-point types. Compared with the floating-point operation, significantly less PL resource is required for implementing an AP fixed-point operation and the latency achieved is also smaller.
Same as the AP integer classes, the ap_fixed<> and ap_ufixed<> classes support many standard binary, unary, logic, and bitwise operations. They also provide many helper methods for printing and conversion to standard C++ types. The details of all these can be found in [AMD-Xilinx24c] or from here.
The Vitis HLS Math Library also implements a subset of math functions with AP fixed-point and AP integer inputs with the following restrictions:
- ap_fixed<W,I> where I \(\leq 33\) and W-I \(\leq 32\)
- ap_ufixed<W,I> where I \(\leq 32\) and W-I \(\leq 32\)
- ap_int<I> where I \(\leq 33\)
- ap_uint<I> where I \(\leq 32\)
- Template parameters Q, O, and N for ap_fixed and ap_ufixed types are not supported.
For example, the AP fixed-point cosine function is simply the overloaded version of hls::cos. The list of math functions implemented can be found here. Compared with their floating-point counterparts, RTL implementations of these fixed-point functions are smaller and faster, but may be slightly less accurate.

4.4.4. Vector Types#

The Vitis HLS Vector Library provides a C++ class template hls::vector<T, N> to vectorize the math data types mentioned above in order to synthesize SIMD-type operations. The template parameters T and N specify the primitive data type and the length of the vector. The header file <hls_vector.h> should be included to use the vector template.
The hls::vector<T, N> class extends standard binary, unary, bitwise, and relational operations of the primitive type T in an elementwise fashion to behave like SIMD operations. Each element in the vector can be assessed using the [] operator just as the elements in an array. Initialization of the vector elements can be performed using the standard C++ array initialization syntax.
Example:
```
#include <hls_vector.h>

typedef hls::vector<int, 100> vint100;

void vadd(vint100 a, vint100 b, vint100 &c) {
  c = a+b;
}
```
Vitis HLS synthesizes 100 adders and 200 registers to hold and add the elements of the vectors a and b in parallel. The RTL design would be similar to the one generated by using int arrays for a and b and performing the addition in a loop with the loop completely unrolled and the arrays completely reshaped. The SIMD addition can be performed in a single clock cycle using a large amount of PL resources.