3.2. Producer-Consumer Model

• In a typical DSP application scenario, a signal source (e.g., an ADC or a camera) provides a stream of samples that is fed into a DSP task (e.g., an FIR filter) for processing. The DSP task may produce an output stream of samples that is in turn fed into another DSP task (e.g., an FFT) for further processing, and so on, eventually reaching a signal sink (e.g., the PS host). We may perform each DSP task in a separate PL kernel, or package all DSP tasks into a single PL kernel in HLS.

• This configuration naturally leads to the producer-consumer model in which a DSP task acts as a producer of samples and another DSP task downstream acts as a consumer of the samples supplied by the producer task. Some form of buffering is typically applied between the producer and consumer. The operation of a DSP kernel may then be described by a directed graph, called the signal/data flow graph, representing a network of connected producer and consumer tasks from the input (source) of the DSP kernel to its output (sink).

• It is advantageous for us to develop our C/C++ design of a DSP kernel following this producer-consumer model because it allows the HLS tool to automate the optimization of pipelining and parallelization at the task level, as explained in the following sections. Pipelining and parallelization can also be applied within a task at the instruction level.

3.2.1. Pipelining

• Task-level pipelining is best explained by considering an example. Suppose the function of a DSP kernel can be decomposed into a sequence of three tasks, namely tasks \(A\), \(B\), and \(C\) in that order. The data flow graph of the DSP kernel is then simply

  (3.1)\[\begin{equation} \boxed{I} \rightarrow A \rightarrow B \rightarrow C \rightarrow \boxed{O} \end{equation}\]

  where \(\boxed{I}\) is the input to the kernel, \(\boxed{O}\) is the kernel output, and each directed edge \(\rightarrow\) shows the direction of the producer-consumer relation and buffering between two connected tasks. The IIs of the three tasks are \(\tau_A\), \(\tau_B\), and \(\tau_C\) clock cycles, respectively. For illustration below, let us assume \(\tau_B > \tau_A > \tau_C\).

• If the producer-consumer model is not followed in the development of the DSP kernel that task \(A\) has to wait for both tasks \(B\) and \(C\) to complete their respective operations on its output unit before it starts to work on another input unit, then both the iteration latency and II of the DSP kernel will be \(\tau_A + \tau_B + \tau_C\), and the throughput cannot be higher than \(\frac{1}{\tau_A + \tau_B + \tau_C}\) output units per clock cycle.

• Under the producer-consumer model, with sufficient buffering between the tasks, instead of sitting idle waiting for the other two downstream tasks to complete their processing on its output, task \(A\) can start processing the next input unit in a pipelining fashion as shown in the figure below:

  

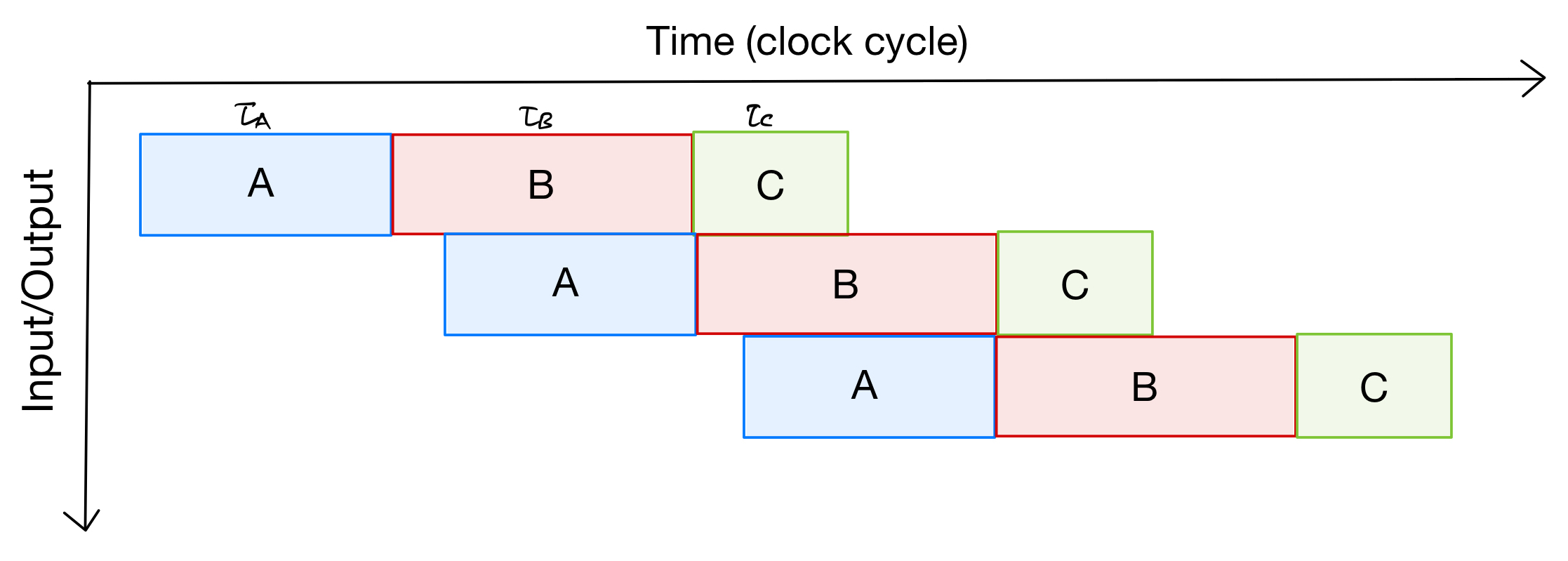
  Fig. 3.1 Timing diagram showing task-level pipelining in a DSP kernel constructed under the producer-consumer model with tasks A, B, and C of different IIs.

  With this form of task-level pipelining, it is easy to check that while the iteration latency of the DSP kernel is still \(\tau_A + \tau_B + \tau_C\), the II drops down to \(\tau_B\) and the throughput increases to \(\frac{1}{\tau_B}\).

• We see from the example above that task-level pipelining can decrease the II and increase the throughput of a DSP kernel while not requiring additional PL resources, except perhaps for additional buffering and more complex control logic. However, task-level pipelining does require the IIs of all tasks to be known at the build time for the HLS tool to construct the pipelining schedule.

3.2.2. Parallelization

• When two DSP tasks are fully independent, i.e., their operations do not depend on one another, they do not communicate, and they do not access any shared memory or computational resource, they can be executed in parallel; thus reducing the II and increasing the throughput of the DSP kernel.

• A piece of C/C++ code written in the producer-consumer model helps the HLS tool to identify opportunities for task-level parallelization. For example, the following data flow graph shows that tasks \(B\) and \(C\) are fully independent and hence can be executed in parallel:

  (3.2)\[\begin{split}\begin{equation} \boxed{I} \rightarrow A \ \begin{array}{c} \nearrow {}^{\displaystyle B} \searrow \\ \searrow {}_{\displaystyle C} \nearrow \end{array} \ D \rightarrow \boxed{O} \end{equation}\end{split}\]

• With task-level parallelization, independent tasks are executed simultaneously on different PL resource. Hence, unlike pipelining, parallelization does require more PL resource usage.

3.2.3. FIFO & PIPO

• For the producer-consumer model to function properly, the producer and consumer tasks need to synchronize with each other. That is, there must be a handshaking process for the producer to tell the consumer that a piece of data is ready to be consumed and after that for the consumer to tell the producer that the piece of data has been consumed. As one would see, such synchronization among producers and consumers in a complex data flow graph could get rather complicated. The synchronization complexity could be further aggravated by pipelining and parallelization as they require different tasks to simultaneosuly operate on different pieces of data.

• The standard solution to this synchronization problem is to insert a streaming buffer between each pair of producer and consumer. The streaming buffer streamlines synchronization between the producer and consumer by allowing the producer to simply push its output data to the buffer (if the buffer is not full) and the consumer to pop its input data (if it is available) from the buffer. No direct handshaking is needed between the producer and consumer. With the streaming buffer, synchronization between each producer-consumer pair in the data flow graph is implicitly achieved, regardless of how complex the data flow graph may be and whether task-level pipelining is employed. Nevertheless, care must be taken in the design process such that the insertion rate of data by the producer into the streaming buffer can not be higher than the retrieving rate of data by the consumer; otherwise, the buffer length will need to grow indefinitely to avoid dropping data or deadlock.

• First-in first-out (FIFO) buffer and ping-pong (PIPO) buffer are the two common implementations for a streaming buffer:

  FIFO

  A FIFO buffer is a queue with a pre-determined depth in which elements must be retrieved (popped) sequentially from the queue in the same order that they are inserted into the queue.

  PIPO

  A PIPO buffer is a pair of buffers with a pre-determined size where one buffer is used to hold a block of the producer’s old output data for the consumer to consume while the producer inserts new data to the other buffer. The roles of the two buffers switch after the consumer finishes consuming the data in the old buffer and producer completes inserting data into the new buffer.

• FIFO vs. PIPO:

  • PL resource usage: A PIPO requires more PL resource than a FIFO of the same size/depth as a PIPO contains a pair of buffers while a FIFO contains a single one.

  • Random access: The data in a FIFO must be accessed sequentially while a PIPO often supports random access of the data.

  • Elementwise access: In a PIPO, the data in a buffer can not be consumed by the consumer until the producer has completed filling up that buffer with its output data. On the other hand, a FIFO does not have this block access restriction in that a piece of data is immediately available for the consumer to access after it has been inserted into the FIFO queue by the producer. This elementwise access capability of the FIFO could be advantageous in reducing the iteration latency and II with pipelining.

  • Simultaneous access: In a PIPO, since the producer accesses one buffer and the consumer accesses the other at any time, they can simultaneously access the PIPO. However, since there is only a single buffer in a FIFO, each element in the FIFO can only be either read or written at a time. Thus, using a PIPO may increase the throughput.

  • Deadlock: The use of FIFOs of insufficient depth in a data flow graph may cause a deadlock (see the discussions in Section 3.3). The use of PIPOs, on the other hand, guarantees the data flow graph to be deadlock-free.