7.7. Polyphase Implementation of Interpolation#

Consider the interpolation system as shown below with an interpolation filter

Interpolation system

whose impulse response is \(h[n] \stackrel{z}{\longleftrightarrow} H(z)\):

  1. Applying the transposed form of the polyphase decomposition identity to \(H(z)\) with \(e_k[n] = h[nU+k]\), for \(k=0,1,\ldots, U-1\), gives

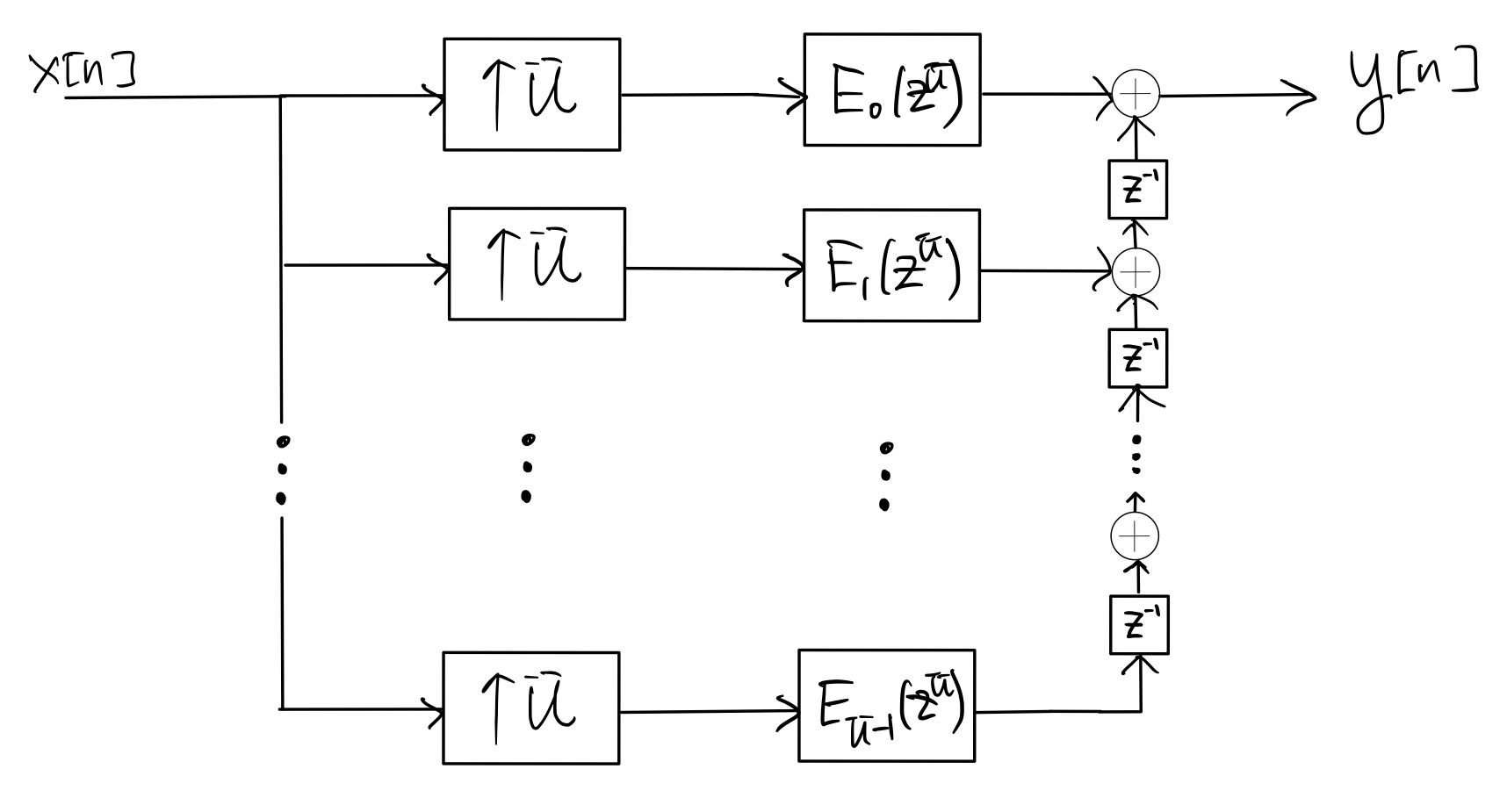
    Polyphase decomposition step 1

  2. Next, applying the upsampling identity to each branch in step 1 gives

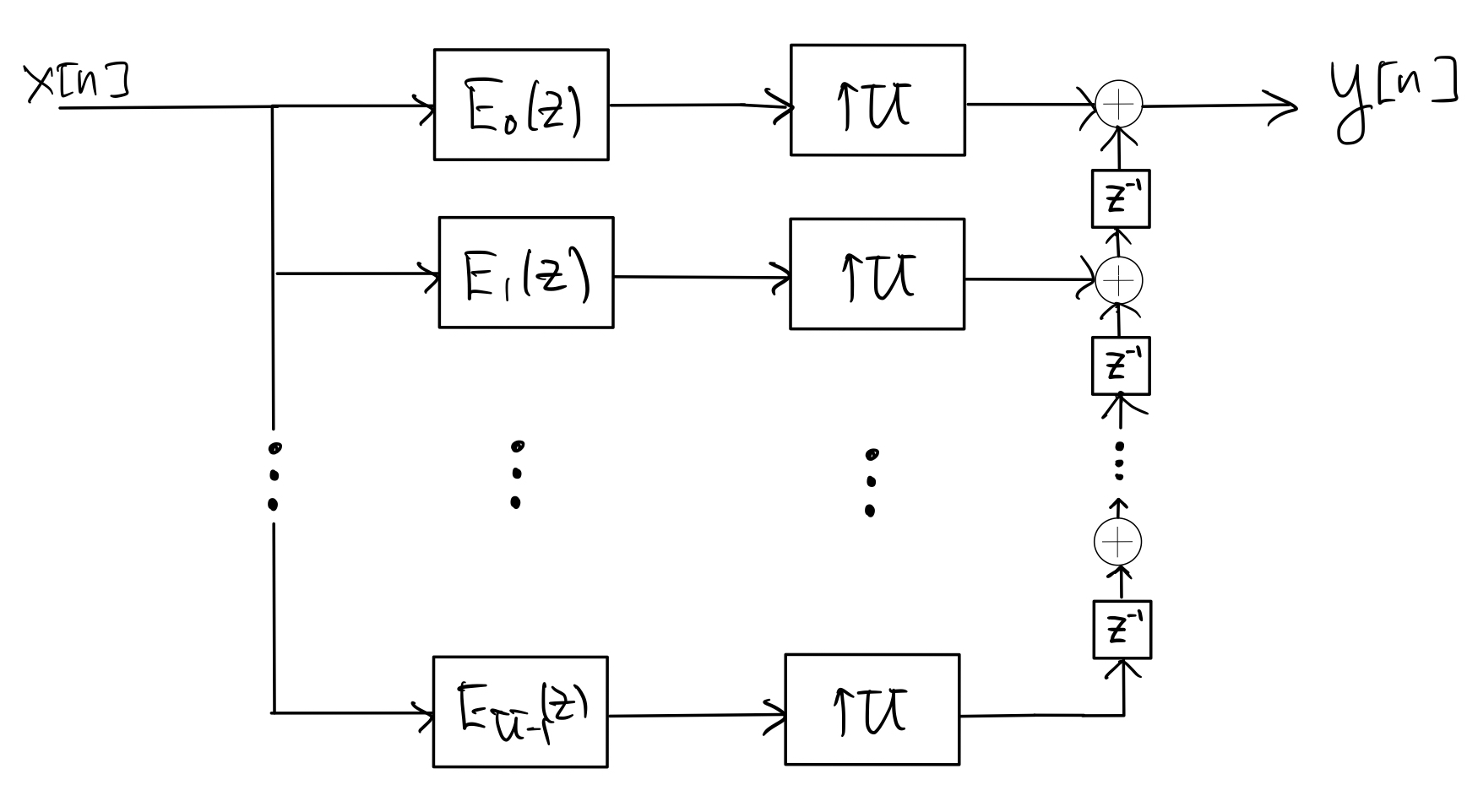
    Polyphase decomposition step 2

  3. Finally, applying the upsample-mux identity to the bank of upsamplers in step 2 gives the following polyphase implementation of the interpolation system:

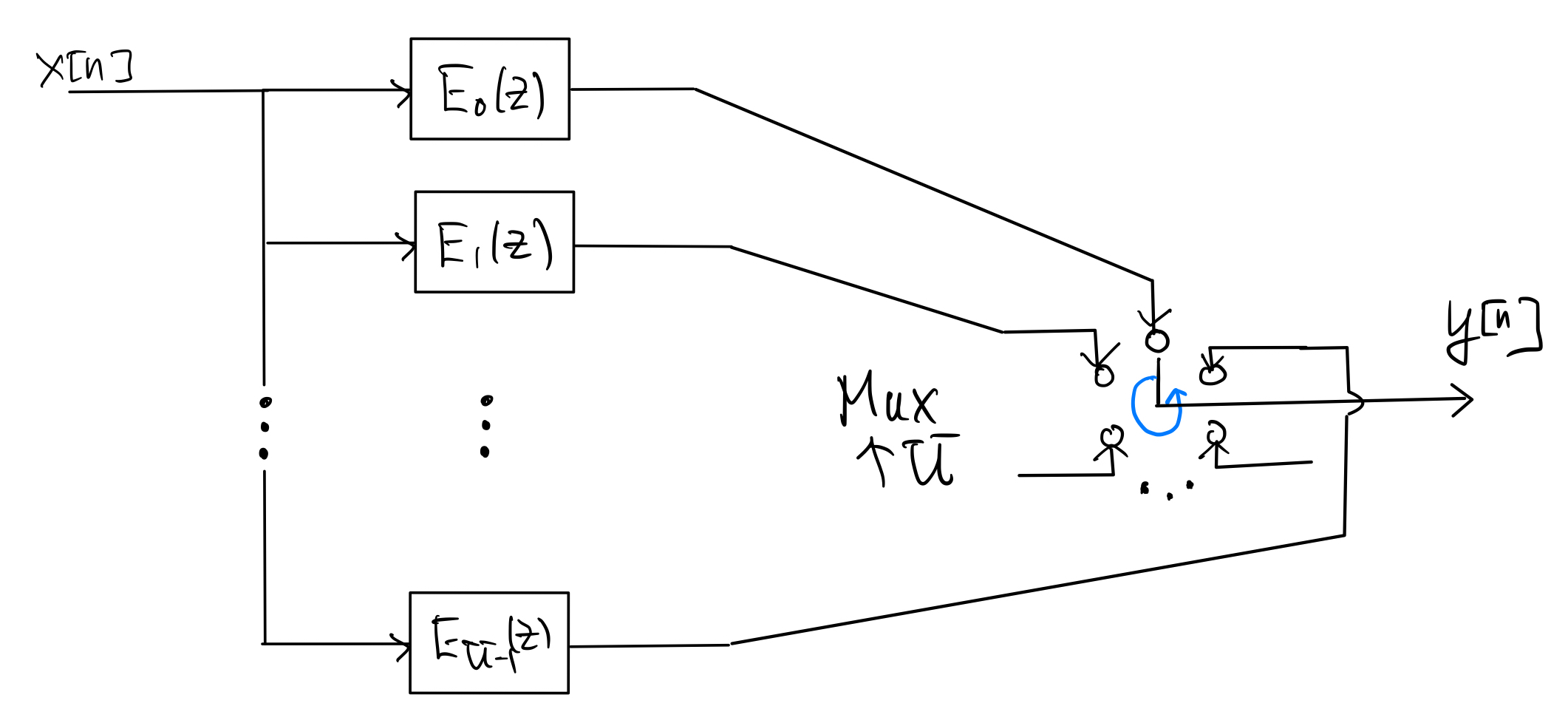
    Polyphase decomposition step 3

  • Note that all the polyphase filters \(E_k(z)\), \(k=0,1,\ldots, U-1\), operate at the input rate. If \(H(z)\) is an FIR filter of length \(L\), then the length of each of the polyphase (FIR) filters is about \(\frac{L}{U}\).

  • Clearly, the polyphase structure allows simple parallel implementation of the polyphase filters. Assuming \(NU \gg L\) where \(N\) is the length of the input signal, the computational complexity (number of multiplications) of the polyphase implementation is \(\mathcal{O}(L)\) per input sample, instead of \(\mathcal{O}(UL)\) per input sample for the direct implementation.