7.6. Polyphase Implementation of Downsampling#

Consider the downsampling system as shown below with an anti-aliasing filter

Downsampling with anti-aliasing filter

whose impulse response is \(h[n] \stackrel{z}{\longleftrightarrow} H(z)\):

  1. Applying the direct form of the polyphase decomposition identity to \(H(z)\) with \(e_k[n] = h[nD+k]\), for \(k=0,1,\ldots, D-1\), gives

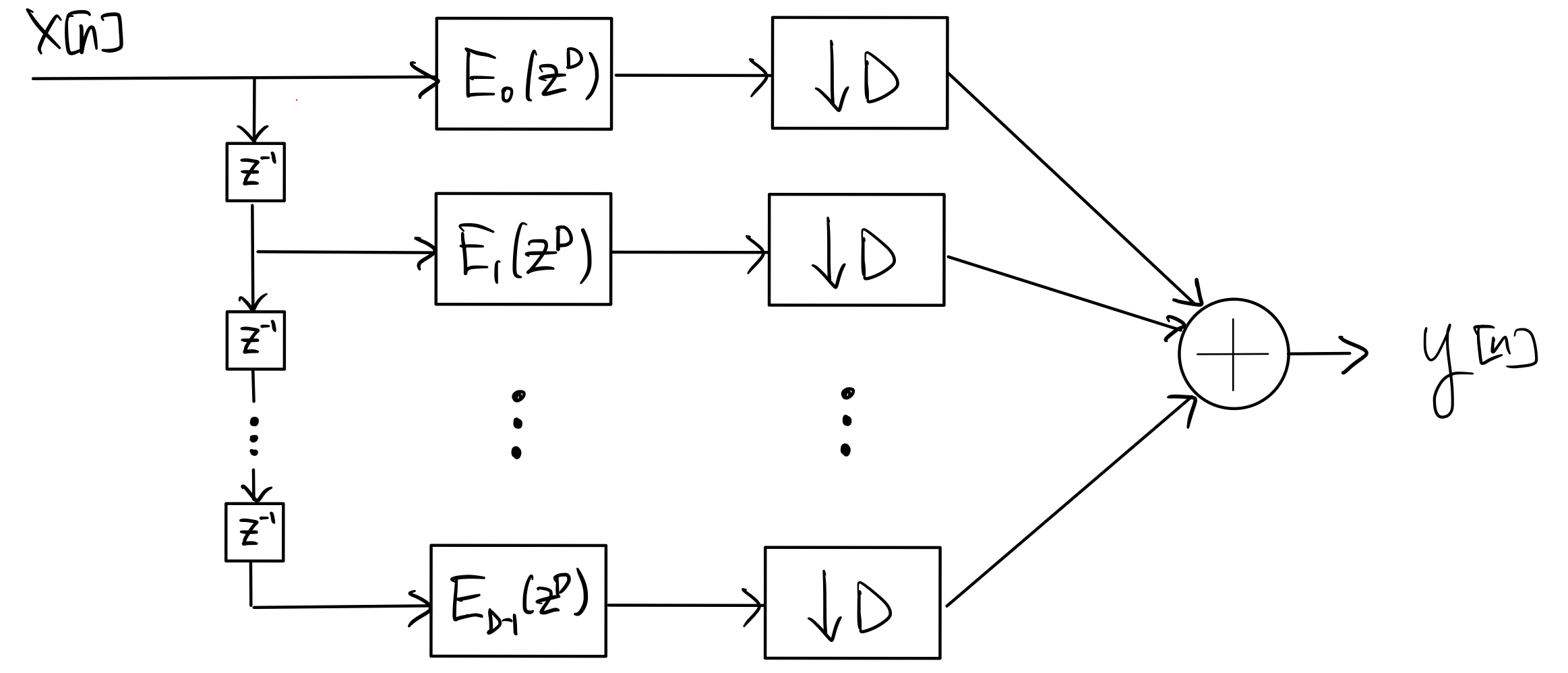
    Polyphase decomposition step 1

  2. Next, applying the downsampling identity to each branch in step 1 gives

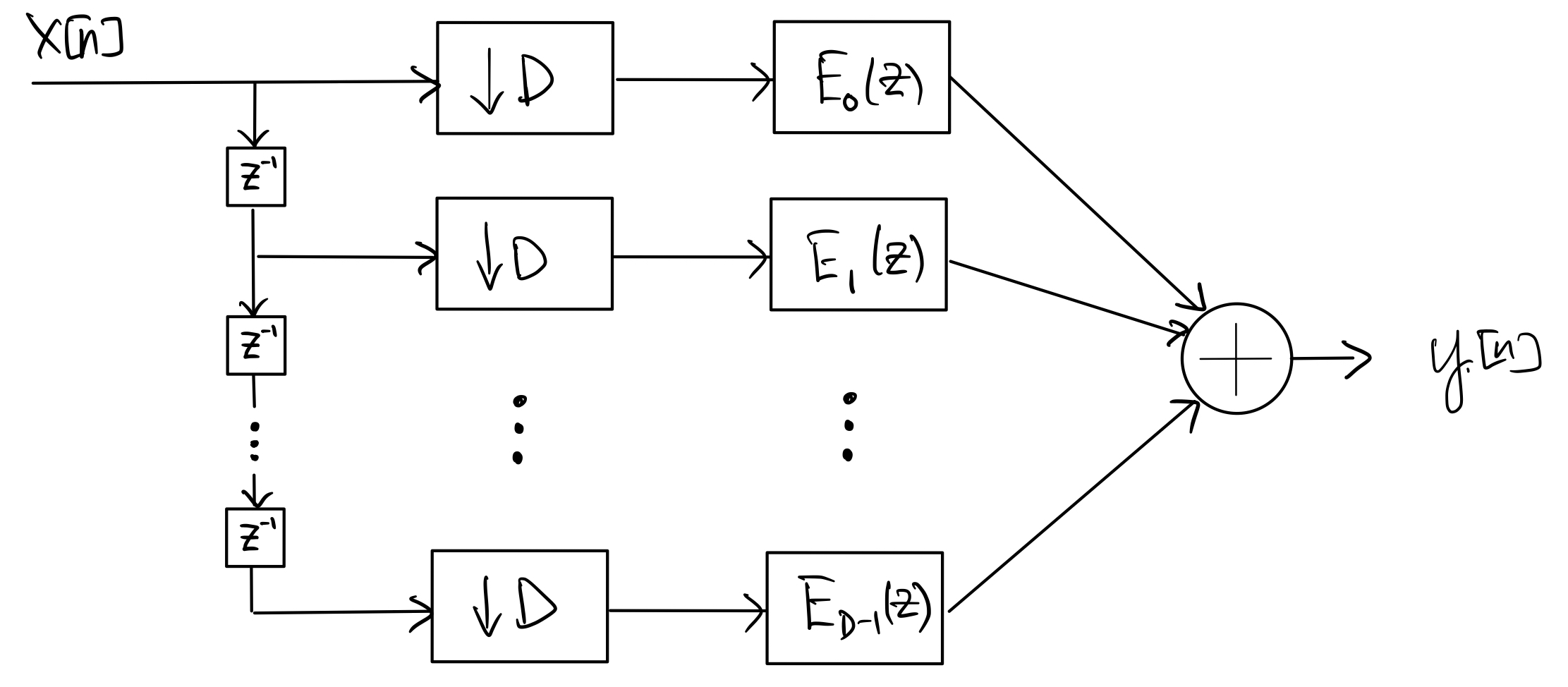
    Polyphase decomposition step 2

  3. Finally, applying the downsample-demux identity to the bank of downsamplers in step 2 gives the following polyphase implementation of the downsampling system:

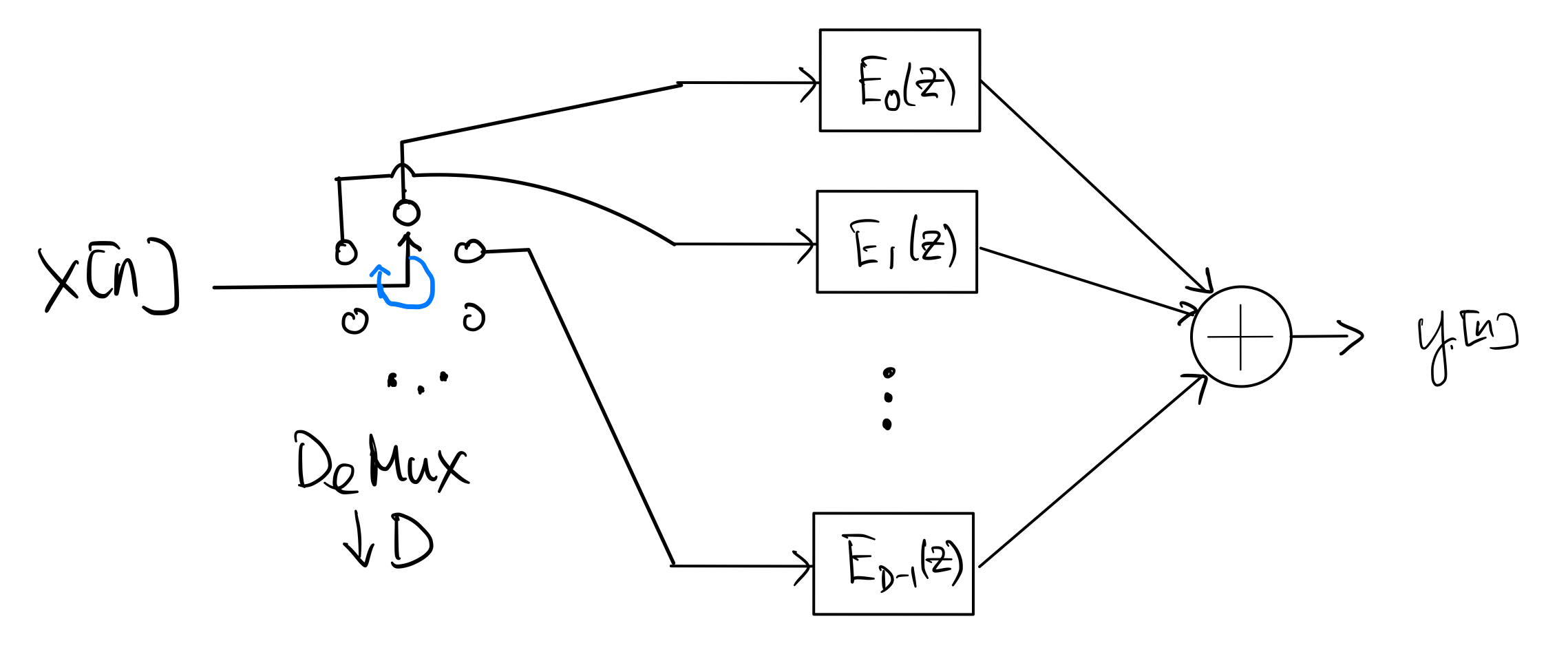
    Polyphase decomposition step 3

  • Note that all the polyphase filters \(E_k(z)\), \(k=0,1,\ldots, D-1\), operate at \(\frac{1}{D}\) times of the input rate. If \(H(z)\) is an FIR filter of length \(L\), then the length of each of the polyphase (FIR) filters is about \(\frac{L}{D}\).

  • Clearly, the polyphase structure allows simple parallel implementation of the polyphase filters. Nevertheless, the computational complexity (number of multiplications) of the polyphase implementation remains \(\mathcal{O}(\frac{L}{D})\) per input sample, assuming time-domain implementation for \(h[n]\) and all polyphase component filters by convolution.