9.4. Non-decision-directed Phase-locked Loop

• For simple discussion, consider only the BPSK constellation \(\{\pm 1\}\) and QPSK constellation \(\{\pm 1, \pm j\}\).

• Suppose first that \(b[n]\)’s are i.i.d. symbols chosen equally likely from an \(M\)-ary constellation of a linear modulation and are unknown to the RX. Then it can be shown that the joint ML estimator for \((\omega_o, \theta)\) becomes

  (9.12)\[\begin{equation} (\hat \omega_o, \hat \theta) \approx \arg\!\max_{\!\!\!\!\omega_o, \theta} \sum_n \ln \left\{ \frac{1}{M} \sum_{i=0}^{M-1} \exp\left[ \frac{1}{N_0}\text{Re} \left( a_i^* \tilde r[n] e^{-j(\omega_o nT+\theta)} \right) \right] \right\} \end{equation}\]

  where \(\tilde r[n] = \left[ r(t) * p^*(-t) \big|_{t=nT} \right]\) and \(\{a_0,a_1, \ldots, a_{M-1}\}\) is the constellation.

• Rewrite \(\phi[n] = \omega_o nT+\theta\) and consider the ML estimate \(\hat\phi[n]\) of \(\phi[n]\):

  • For BPSK, the decision statistic in (9.12) simplifies to

    \[\begin{equation*} \sum_n \ln\cosh \left[ \frac{1}{N_0}\text{Re} \left( \tilde r[n] e^{-j\phi[n]} \right) \right]. \end{equation*}\]

  • For QPSK, it simplifies to

    \[\begin{equation*} \sum_n \ln\cosh \left[ \frac{1}{N_0}\text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \left(\phi[n] -\frac{\pi}{4} \right)} \right) \right] + \ln\cosh \left[ \frac{1}{N_0}\text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \left(\phi[n] + \frac{\pi}{4} \right)} \right) \right]. \end{equation*}\]

• As before, set the derivative of the decision statistic in (9.12) w.r.t. \(\phi[n]\) to 0 as before, we may solve for \(\hat\phi[n]\) in the following equations:

  • BPSK:

    (9.13)\[\begin{equation} \sum_n \text{Re} \left( \tilde r[n] e^{-j \left(\hat\phi[n] + \frac{\pi}{2} \right)} \right) \tanh \left[ \frac{1}{N_0}\text{Re} \left( \tilde r[n] e^{-j\hat\phi[n]} \right) \right] = 0 \end{equation}\]

  • QPSK:

    (9.14)\[\begin{equation} \sum_n \text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \left(\tilde\phi[n] +\frac{\pi}{2} \right)} \right) \tanh \left[ \frac{1}{N_0}\text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \tilde\phi[n]} \right) \right] - \text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \tilde\phi[n]} \right) \tanh \left[ \frac{1}{N_0}\text{Re} \left( \frac{\tilde r[n]}{\sqrt{2}} e^{-j \left(\tilde\phi[n] + \frac{\pi}{2} \right)} \right) \right] =0 \end{equation}\]

    where \(\tilde \phi [n] \triangleq \hat\phi[n] - \frac{\pi}{4}\).

• For high SNR (\(\frac{1}{N_0} \gg 1\)), using the approximation \(\tanh(x) \approx \text{sgn}(x)\) if \(|x| \gg 1\) in (9.13) and (9.14) shows that the following PLL can be used to track \(\phi[n]\):

  

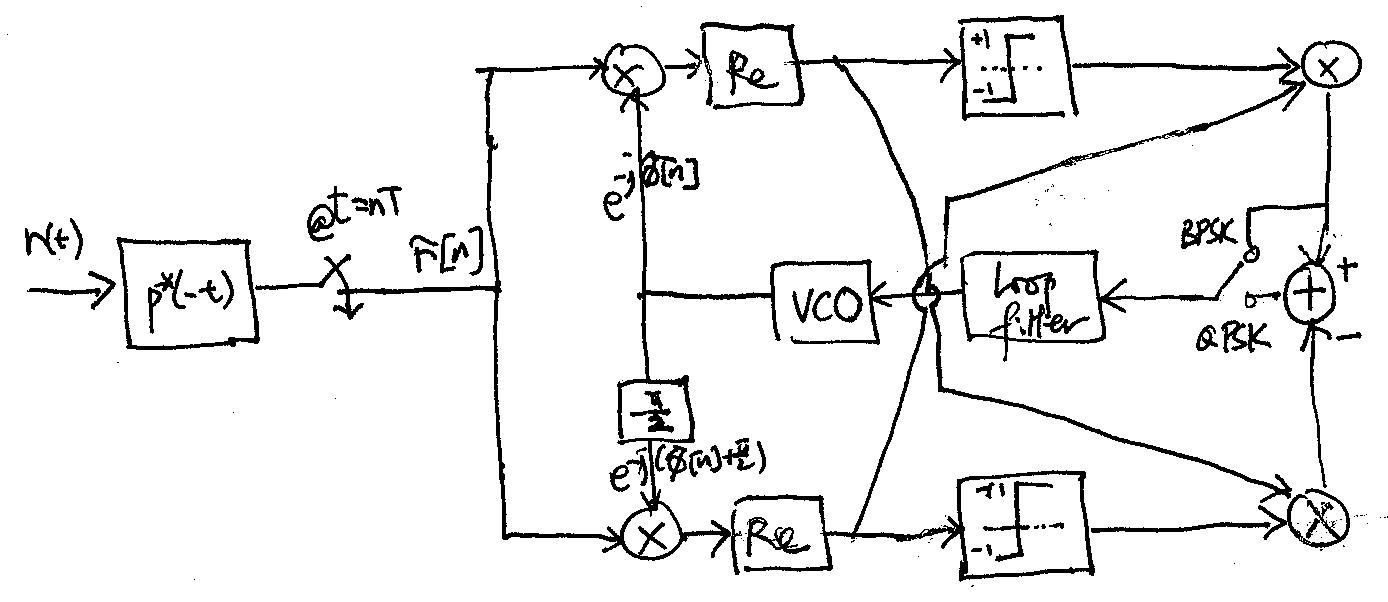
  This PLL is an instance of a class of non-decision-directed PLLs called the Costas loops. Note that the loop settles at \(\hat\phi[n] - \frac{\pi}{4}\) for QPSK.

• For low SNR (\(\frac{1}{N_0} \ll 1\)), using the approximation \(\tanh(x) \approx x\) if \(|x| \ll 1\) in (9.13) and (9.14) shows that the Costas loop above with the hard-limiters removed can be used to track \(\phi[n]\).

• It is easy to check that the phase function estimates provided by the Costas loops (high and low SNR) above have a phase ambiguity of \(\pi\) for BPSK, and \(\pi\) or \(\pm \frac{\pi}{2}\) for QPSK.

9.4.1. USRP implementation

Using a second-order loop filter, the algorithms in (9.10) or (9.11) can be used to implement the Costas loop above with the following modifications:

• BPSK:

  \[\begin{align*} \phi[n] &= \angle \tilde r[n]\\ \phi_e[n] &= \begin{cases} \phi[n] - \hat\phi[n] + \pi & \text{if } -\pi \leq \phi[n] - \hat\phi[n] < -\frac{\pi}{2} \\ \phi[n] - \hat\phi[n] & \text{if } -\frac{\pi}{2} \leq \phi[n] - \hat\phi[n] < \frac{\pi}{2} \\ \phi[n] - \hat\phi[n] -\pi & \text{if } \frac{\pi}{2} \leq \phi[n] - \hat\phi[n] < \pi \end{cases}. \end{align*}\]

• QPSK:

  \[\begin{align*} \phi[n] &= \angle \tilde r[n] \\ \phi_e[n] &= \begin{cases} \phi[n] - \hat\phi[n] + \pi & \text{if } -\pi \leq \phi[n] - \hat\phi[n] < -\frac{3\pi}{4} \\ \phi[n] - \hat\phi[n] +\frac{\pi}{2} & \text{if } -\frac{3\pi}{4} \leq \phi[n] - \hat\phi[n] < -\frac{\pi}{4} \\ \phi[n] - \hat\phi[n] & \text{if } -\frac{\pi}{4} \leq \phi[n] - \hat\phi[n] < \frac{\pi}{4} \\ \phi[n] - \hat\phi[n] -\frac{\pi}{2} & \text{if } \frac{\pi}{4} \leq \phi[n] - \hat\phi[n] < \frac{3\pi}{4} \\ \phi[n] - \hat\phi[n] -\pi & \text{if } \frac{3\pi}{4} \leq \phi[n] - \hat\phi[n] < \pi \end{cases}. \end{align*}\]